InfoHub Logo

Shyǵys Qazaqstan oblysy Semeı qalasy
Semeı qalasynyń Shákárim atyndaǵy memlekettik ýnıversıtetiniń
«5V010900» - matematıka mamandyǵynyń stýdentteri
Nýrlanova Elnara, Abdısamatova Gýldana   
Ǵylymı jetekshisi – Q. R. Taıboldına

Anotasıa

Maqala mektep matematıka kýrsynda ırasıonal teńdeýler men teńsizdikterdi oqytýdyń erekshelikterine arnalǵan. Arnaıy esepter shyǵarý joldary kómegimen osy taqyrypty  oqytýdyń erekshelikterimen jáne kezeńderimen tanysýǵa erekshe kóńil bólinedi.

Kilt sózder: mekteptegi ırasıonal teńdeýler men teńsizdikter, teńdeýler men teńsizdikter júıesi, anyqtalý oblysy.

Teńdeýler uǵymymen oqýshylar tómengi synyptardan tanys. Bútin koeffsentti algebralyq, bólshek rasıonal, qarapaıym trıgonometrıalyq jáne ırasıonal teńdeýler men teńsizdikterdi sheshý kóp qıyndyq týdyrmaıdy. Al teńdeýler túbirleriniń rasıonal ne ırasıonal bolatyndyǵyn, olardyń koeffısısentterine baılanysty teńdeýdiń túbirleri bar ne joǵyn anyqtaý, teńdeý sheshimin tabý úshin onyń anyqtalý oblysyn eskere otyryp túrlendirý oqýshylar úshin birshama qıyndyqtar týdyratyndyǵy belgili.

Teńdeýler men teńsizdikterdiń sheshimin izdestirýde órnektiń anyqtalý oblysynyń mańyzy zor. "Anyqtalý oblysy" túsinigi "fýnksıa" uǵymmen tyǵyz baılanysgy.

Teńdeýler men teńsizdikterdi sheshý barysynda fýnksıanyń berilý jıyny men olardyń qıylysýy, ártúrli túrleńdirýler t.s.s. basqa da maǵlumattar men túsinikter qamtylady jáne olardyn barlyǵy logıkalyq taldaýlar turǵysynda júzege asyrylady.

Eger berilgen teńdeýdiń árbir sheshimi ekinshi bir teńdeýdiń de sheshimi bolsa onda ekinshi teńdeý berilgen teńdeýdiń saldary dep ataldy.

Eger eki teńdeýdiń biriniń sheshimi ekinshisiniń de sheshimi bolsa onda ol teńdeýler mándes(ekvıvalentti) dep atalady.

Berilgen teńdeýden onyn saldary bolatyn teńdeý alý úshin kelesi amaldardy oryndaýǵa bolady:

1) teńdeýdiń eki jaǵyna, onyń anyqtalý oblysynda anyqtalǵan fýnksıany qosýǵa nemese shegerýge jáne kóbeıtýge;

2) teńdeýdiń eki jaǵyn, onyń anyqtalý oblysynda anyqtalǵan nólge teń emes fýnksıada bólýge;

3) eger g₁(x)*g₂(x)*...*g_n(x)=0 túrindegi teńdeý berilse, onda kelesi teńdeýler jıyntyǵy, onyń saldary bolady:

g₁(x)=0, g₂(x)=0, ... , g_n(x)=0

Tendeýlerdi túrlendirý kezinde onyń anyqtalý oblysy ózgerýi múmkin. Sondyqtan tabylǵan sheshimderdi berilgen teńdeýge qoıyp tekserý kerek.

Berilgen teńdeýden onymen mándes (ekvıvalentti) teńdeýge kóshý úshin kelesi amaldardy oryndaýǵa bolady:

1) teńdeýdiń eki jaǵyna, onyń anyqtalý oblysynda anyqtalǵan fýnksıany qosýǵa nemese eki jaǵynan shegerýge;

2) teńdeýdiń eki jaǵyn da, onyń anyqtalý oblysynda anyqtalǵan nólge teń emes fýnksıaǵa kóbeıtýge ne bólýge;

3) teńdeýdiń eki jaǵyn tak dárejege shyǵarýǵa;

4) eger teńdeýdiń eki jaǵyndaǵy fýnksıalardyń mánderi teris emes bolsa, onda eki jaǵyn jup dárejege shyǵarýǵa.

Irasıonal teńdeýlerge qatysty kelesideı kesteni usynýǵa bolady.

Irasıonal teńdeýlerdi sheshý barysynda kelesi amaldardy jasaýǵa bolmaıdy:

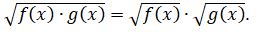Bul amal teńdeýdiń anyqtalý oblysyn taryltady.

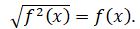Bul teńdik tek qana 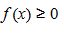bolǵanda oryndy. Jalpy jaǵdaıda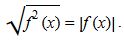

Endi atalǵan taqyrypqa qatysy birneshe esepterdi qarastyraıyq.

l. 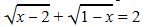 teńdeýin sheshińiz.

Sheshýi. Bul teńdeýdi eki jaǵyn da kvadrattaý nemese teńdeýler júıesine keltirý ádisterimen sheshýge bolady. Osy ádisterdiń árqaısysy da birshama esepteýler júrgizýdi qajet etedi. Kúrdeli esepteýlersiz teńdeýdiń sheshimin anyqtaýǵa múmkindik beretin ádisti qarastyraıyk. Osy maqsatta, fýnksıanyń anyqtalý oblysyn tabamyz. Ol kelesi teńsizdikter júıesiniń sheshimi:

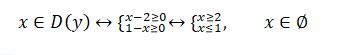
Iaǵnı, 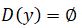 teńdeýdiń sheshimi joq.

Keıde anyqtalý oblysy aqyrly núkteler jıynynan turady, ondaı jaǵdaıda teńdeýdiń sheshimi bolsh tabylatyndaryn olardyń arasynan tekserip, tańdaý ǵana jetkilikti. Al keı jaǵdaılarda anyqtalý oblysy aqyrly núkteler jıynynan turmaıdy, sondyktan bip qaraǵanda, teńdeý anyqtalý oblysyn zertteý jolymen sheshilmeıtin bolyp kórinedi. Biraq anyqtalý oblysyn tabý tásilin teńdeýdi sheshýdiń ár qadamynda qoldanýǵa bolady.

2. 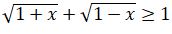 teńsizdigin sheshińiz.

Sheshýi. 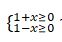  teńsizdikter júıesiniń sheshimi  -1≤ h≤ 1 ekendigin kórý qıyn emes. Iaǵnı, berilgen órnektiń anyqtalý oblysy  -1≤ h≤ 1

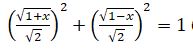bolǵandyqtan, 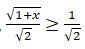nemese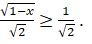

Sondyqtan, 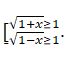. Onda  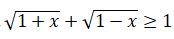teńsizdigi anyqtalý oblysyna tıisti barlyq  x úshin oryndalady. Demek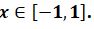

3. 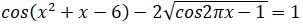 tendeýin júıesin sheshińiz.

Sheshýi. Teńdeýdiń tikeleı anyqtaý múmkin emestikten, anyqtalý oblysyn tabaıyq. Ol úshin cos2πh-1≥ 0 , ıaǵnı cos2πh≥ 1 teńsizdiginiń sheshimderin anyqtaý kerek. Sońǵy teńsizdikten cos2πh=1 bolatyndyǵy aıqyn. Sonymen, anyqtalý oblysy h=k, k∈Z . Tabylǵan mánderdi berilgen teńdeýge qoıyp, ony qanaǵattandyratyndaryn anyqtaıyq. Sonda cos(k²+k-6) =1 teńdeýin alamyz. Osydan (k²+k-6) = 2πn, mundaǵy . n, k∈Z Sońǵy teńdeýdiń sol jaǵyndaǵy órnek bútin san, al oń jaǵyndaǵysy bútin emes ekendigin kóremiz. Sondyqtan teńdik tek qana n = 0 bolǵanda oryndalýy múmkin.

Endi (k²+k-6) = 0 teńdeýin sheshemiz. Onyń túbirleri k = 2 jáne k = -3 . Demek, tendeýdiń sheshinderi x = 2 jáne x = -3 .

Biz buǵan deıin teńdeýler men teńsizdikterdi sheshýde anyqgalý oblysyna kóńil bóldik. Biraq osy ádisti qoldanýǵa kelmeıtin tapsyrmalar da kezdesedi. Keı jaǵdaıda ırasıonal tendeýler men teńsizdikterdiń sheshimin anyqtaý úshin, túıindesine kóbeıtý ádisin qoldanýǵa bolady

4. 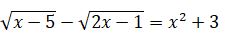teńdeýin sheshińiz.

Sheshýi.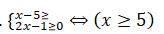

Teńsizdikter júıesi dep qarastyrsaq, qate jibergen bolar edik. Sebebi teńdeýdiń oń jaq bóligi eskerilmeı otyr. Ol nolden úlken, sondyqtan teńdeýdiń anyqtalý oblysy kelesi teńsizdikter júıesiniń sheshimi bolady:

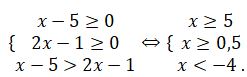
Demek, teńdeýdiń sheshimi joq.

5. 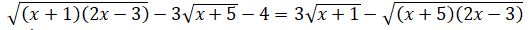 teńdeýin sheshemiz.

Sheshýi. Teńdeýdiń eki jaǵyn kvadrattasaq berilgen teńdeýden de kúrdeli teńdeý alamyz. Sondyqtan, berilgen teńdeýdi kelesideı túrlendireıik: 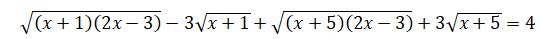Teńdeýdiń col jaǵyndaǵy órnekti kóbeıtkishterge jiktesek  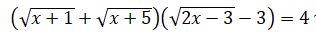teńdeýine kelemiz. Ádette, tendeýdiń oń jaǵynda 0 bolǵanda kóbeıtkishterge jikteıdi. Berilgen teńdeý jaǵdaıynda koeffısentterge baılanysty, teńdeýdiń sheshimi jeńil tabylady. Sońǵy teńdeýdiń eki jaǵyn da birinshi jaqshadaǵy órnektiń túıindesine kóbeıteıik, ıaǵnı,  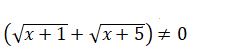órnegine. Onda  

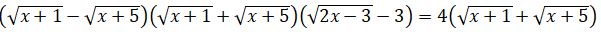Osydan  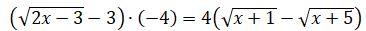nemese  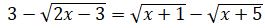bolady. Sońǵy teńdeýdiń eki jaǵyn da kvadrattasaq  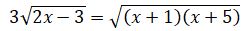teńdeýine kelemiz. Basqasha toptastyryp kvadrattaý, berilgen teńdeýden de kúrdeli teńdeýge ákeledi. Sońǵy teńdeýdiń eki jaǵyn da kvadrattap,

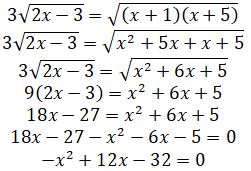
x² -12x +32 = 0 teńdeýin alamyz. Osydan, x = 8 jáne x = 4. Tabylǵan sheshimderdi teńdeýge qoıyp tekserip, onyń sheshimi x = 8 ekendigin kóremiz.

Irasıonal teńdeýler men teńsizdikterdi sheshýdiń joldaryn taldaýda mektep matematıkasynyń negizgi teorıalyq materıaly qamtylady. Taqyrypty durys meńgerý úshin teńdeýler klassıfıkasıalanyp, olardyń árqaısysy boıynsha ony sheshýdiń ádis-tásilderi tańdalyp, meńgerilý deńgeıi tekseriletindigi belgili. Muqıat iriktelip, múmkindiginshe tolyq baıandalǵan teorıalyq materıal, esep qoıylymyn jáne ony sheshýdiń tásilderin úırenýdi qamtamasyz etýmen qatar, qatań logıkalyq taldaýlardy meńgerýde de septigi tıer degen oıdamyz.

Paıdalanǵan ádebıetter:

1. «Samuryq» matematıkalyq zıatkerlik saıysyna berilgen esepterdi shyǵarýǵa arnalǵan ádistemelik qural (5-7 synyp)
2. A. I Prılepko «Sbornık zadach po matımatıke» Moskva, 1983
3. Z. K Aınazarova «Spravochnık shkolnıka po matematıke», «Arman-PV», 2007j

---