InfoHub Logo

شىعىس قازاقستان وبلىسى سەمەي قالاسى
سەمەي قالاسىنىڭ شاكارىم اتىنداعى مەملەكەتتىك ۋنيۆەرسيتەتىنىڭ
«5ۆ010900» - ماتەماتيكا ماماندىعىنىڭ ستۋدەنتتەرى
نۋرلانوۆا ەلنارا، ابديساماتوۆا گۋلدانا   
عىلىمي جەتەكشىسى – ق. ر. تايبولدينا

اننوتاسيا

ماقالا مەكتەپ ماتەماتيكا كۋرسىندا يرراسيونال تەڭدەۋلەر مەن تەڭسىزدىكتەردى وقىتۋدىڭ ەرەكشەلىكتەرىنە ارنالعان. ارنايى ەسەپتەر شىعارۋ جولدارى كومەگىمەن وسى تاقىرىپتى  وقىتۋدىڭ ەرەكشەلىكتەرىمەن جانە كەزەڭدەرىمەن تانىسۋعا ەرەكشە كوڭىل بولىنەدى.

كىلت سوزدەر: مەكتەپتەگى يرراسيونال تەڭدەۋلەر مەن تەڭسىزدىكتەر، تەڭدەۋلەر مەن تەڭسىزدىكتەر جۇيەسى، انىقتالۋ وبلىسى.

تەڭدەۋلەر ۇعىمىمەن وقۋشىلار تومەنگى سىنىپتاردان تانىس. ءبۇتىن كوەففسەنتتى الگەبرالىق، بولشەك راسيونال، قاراپايىم تريگونومەتريالىق جانە يرراسيونال تەڭدەۋلەر مەن تەڭسىزدىكتەردى شەشۋ كوپ قيىندىق تۋدىرمايدى. ال تەڭدەۋلەر تۇبىرلەرىنىڭ راسيونال نە يرراسيونال بولاتىندىعىن، ولاردىڭ كوەففيسيسەنتتەرىنە بايلانىستى تەڭدەۋدىڭ تۇبىرلەرى بار نە جوعىن انىقتاۋ، تەڭدەۋ شەشىمىن تابۋ ءۇشىن ونىڭ انىقتالۋ وبلىسىن ەسكەرە وتىرىپ تۇرلەندىرۋ وقۋشىلار ءۇشىن ءبىرشاما قيىندىقتار تۋدىراتىندىعى بەلگىلى.

تەڭدەۋلەر مەن تەڭسىزدىكتەردىڭ شەشىمىن ىزدەستىرۋدە ورنەكتىڭ انىقتالۋ وبلىسىنىڭ ماڭىزى زور. "انىقتالۋ وبلىسى" تۇسىنىگى "فۋنكسيا" ۇعىممەن تىعىز بايلانىسگى.

تەڭدەۋلەر مەن تەڭسىزدىكتەردى شەشۋ بارىسىندا فۋنكسيانىڭ بەرىلۋ جيىنى مەن ولاردىڭ قيىلىسۋى، ءارتۇرلى تۇرلەڭدىرۋلەر ت.س.س. باسقا دا ماعلۇماتتار مەن تۇسىنىكتەر قامتىلادى جانە ولاردىن بارلىعى لوگيكالىق تالداۋلار تۇرعىسىندا جۇزەگە اسىرىلادى.

ەگەر بەرىلگەن تەڭدەۋدىڭ ءاربىر شەشىمى ەكىنشى ءبىر تەڭدەۋدىڭ دە شەشىمى بولسا وندا ەكىنشى تەڭدەۋ بەرىلگەن تەڭدەۋدىڭ سالدارى دەپ اتالدى.

ەگەر ەكى تەڭدەۋدىڭ ءبىرىنىڭ شەشىمى ەكىنشىسىنىڭ دە شەشىمى بولسا وندا ول تەڭدەۋلەر ماندەس(ەكۆيۆالەنتتى) دەپ اتالادى.

بەرىلگەن تەڭدەۋدەن ونىن سالدارى بولاتىن تەڭدەۋ الۋ ءۇشىن كەلەسى امالداردى ورىنداۋعا بولادى:

1) تەڭدەۋدىڭ ەكى جاعىنا، ونىڭ انىقتالۋ وبلىسىندا انىقتالعان فۋنكسيانى قوسۋعا نەمەسە شەگەرۋگە جانە كوبەيتۋگە؛

2) تەڭدەۋدىڭ ەكى جاعىن، ونىڭ انىقتالۋ وبلىسىندا انىقتالعان نولگە تەڭ ەمەس فۋنكسيادا بولۋگە؛

3) ەگەر g₁(x)*g₂(x)*...*g_n(x)=0 تۇرىندەگى تەڭدەۋ بەرىلسە، وندا كەلەسى تەڭدەۋلەر جيىنتىعى، ونىڭ سالدارى بولادى:

g₁(x)=0، g₂(x)=0، ... ، g_n(x)=0

تەندەۋلەردى تۇرلەندىرۋ كەزىندە ونىڭ انىقتالۋ وبلىسى وزگەرۋى مۇمكىن. سوندىقتان تابىلعان شەشىمدەردى بەرىلگەن تەڭدەۋگە قويىپ تەكسەرۋ كەرەك.

بەرىلگەن تەڭدەۋدەن ونىمەن ماندەس (ەكۆيۆالەنتتى) تەڭدەۋگە كوشۋ ءۇشىن كەلەسى امالداردى ورىنداۋعا بولادى:

1) تەڭدەۋدىڭ ەكى جاعىنا، ونىڭ انىقتالۋ وبلىسىندا انىقتالعان فۋنكسيانى قوسۋعا نەمەسە ەكى جاعىنان شەگەرۋگە؛

2) تەڭدەۋدىڭ ەكى جاعىن دا، ونىڭ انىقتالۋ وبلىسىندا انىقتالعان نولگە تەڭ ەمەس فۋنكسياعا كوبەيتۋگە نە بولۋگە؛

3) تەڭدەۋدىڭ ەكى جاعىن تاك دارەجەگە شىعارۋعا؛

4) ەگەر تەڭدەۋدىڭ ەكى جاعىنداعى فۋنكسيالاردىڭ ماندەرى تەرىس ەمەس بولسا، وندا ەكى جاعىن جۇپ دارەجەگە شىعارۋعا.

يرراسيونال تەڭدەۋلەرگە قاتىستى كەلەسىدەي كەستەنى ۇسىنۋعا بولادى.

يرراسيونال تەڭدەۋلەردى شەشۋ بارىسىندا كەلەسى امالداردى جاساۋعا بولمايدى:

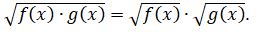بۇل امال تەڭدەۋدىڭ انىقتالۋ وبلىسىن تارىلتادى.

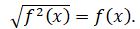بۇل تەڭدىك تەك قانا 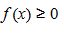بولعاندا ورىندى. جالپى جاعدايدا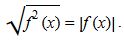

ەندى اتالعان تاقىرىپقا قاتىسى بىرنەشە ەسەپتەردى قاراستىرايىق.

l. 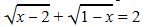 تەڭدەۋىن شەشىڭىز.

شەشۋى. بۇل تەڭدەۋدى ەكى جاعىن دا كۆادراتتاۋ نەمەسە تەڭدەۋلەر جۇيەسىنە كەلتىرۋ ادىستەرىمەن شەشۋگە بولادى. وسى ادىستەردىڭ ءارقايسىسى دا ءبىرشاما ەسەپتەۋلەر جۇرگىزۋدى قاجەت ەتەدى. كۇردەلى ەسەپتەۋلەرسىز تەڭدەۋدىڭ شەشىمىن انىقتاۋعا مۇمكىندىك بەرەتىن ءادىستى قاراستىرايىك. وسى ماقساتتا، فۋنكسيانىڭ انىقتالۋ وبلىسىن تابامىز. ول كەلەسى تەڭسىزدىكتەر جۇيەسىنىڭ شەشىمى:

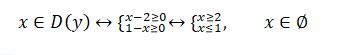
ياعني، 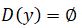 تەڭدەۋدىڭ شەشىمى جوق.

كەيدە انىقتالۋ وبلىسى اقىرلى نۇكتەلەر جيىنىنان تۇرادى، ونداي جاعدايدا تەڭدەۋدىڭ شەشىمى بولش تابىلاتىندارىن ولاردىڭ اراسىنان تەكسەرىپ، تاڭداۋ عانا جەتكىلىكتى. ال كەي جاعدايلاردا انىقتالۋ وبلىسى اقىرلى نۇكتەلەر جيىنىنان تۇرمايدى، سوندىكتان ءبىp قاراعاندا، تەڭدەۋ انىقتالۋ وبلىسىن زەرتتەۋ جولىمەن شەشىلمەيتىن بولىپ كورىنەدى. ءبىراق انىقتالۋ وبلىسىن تابۋ ءتاسىلىن تەڭدەۋدى شەشۋدىڭ ءار قادامىندا قولدانۋعا بولادى.

2. 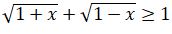 تەڭسىزدىگىن شەشىڭىز.

شەشۋى. 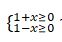  تەڭسىزدىكتەر جۇيەسىنىڭ شەشىمى  -1≤ ح≤ 1 ەكەندىگىن كورۋ قيىن ەمەس. ياعني، بەرىلگەن ورنەكتىڭ انىقتالۋ وبلىسى  -1≤ ح≤ 1

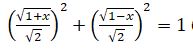بولعاندىقتان، 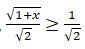نەمەسە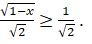

سوندىقتان، 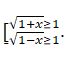. وندا  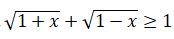تەڭسىزدىگى انىقتالۋ وبلىسىنا ءتيىستى بارلىق  x ءۇشىن ورىندالادى. دەمەك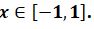

3. 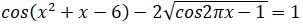 تەندەۋىن جۇيەسىن شەشىڭىز.

شەشۋى. تەڭدەۋدىڭ تىكەلەي انىقتاۋ مۇمكىن ەمەستىكتەن، انىقتالۋ وبلىسىن تابايىق. ول ءۇشىن cos2πح-1≥ 0 ، ياعني cos2πح≥ 1 تەڭسىزدىگىنىڭ شەشىمدەرىن انىقتاۋ كەرەك. سوڭعى تەڭسىزدىكتەن cos2πح=1 بولاتىندىعى ايقىن. سونىمەن، انىقتالۋ وبلىسى ح=k، k∈Z . تابىلعان ماندەردى بەرىلگەن تەڭدەۋگە قويىپ، ونى قاناعاتتاندىراتىندارىن انىقتايىق. سوندا cos(k²+k-6) =1 تەڭدەۋىن الامىز. وسىدان (k²+k-6) = 2πn، مۇنداعى . n، k∈Z سوڭعى تەڭدەۋدىڭ سول جاعىنداعى ورنەك ءبۇتىن سان، ال وڭ جاعىنداعىسى ءبۇتىن ەمەس ەكەندىگىن كورەمىز. سوندىقتان تەڭدىك تەك قانا n = 0 بولعاندا ورىندالۋى مۇمكىن.

ەندى (k²+k-6) = 0 تەڭدەۋىن شەشەمىز. ونىڭ تۇبىرلەرى k = 2 جانە k = -3 . دەمەك، تەندەۋدىڭ شەشىندەرى x = 2 جانە x = -3 .

ءبىز بۇعان دەيىن تەڭدەۋلەر مەن تەڭسىزدىكتەردى شەشۋدە انىقگالۋ وبلىسىنا كوڭىل بولدىك. ءبىراق وسى ءادىستى قولدانۋعا كەلمەيتىن تاپسىرمالار دا كەزدەسەدى. كەي جاعدايدا يرراسيونال تەندەۋلەر مەن تەڭسىزدىكتەردىڭ شەشىمىن انىقتاۋ ءۇشىن، تۇيىندەسىنە كوبەيتۋ ءادىسىن قولدانۋعا بولادى

4. 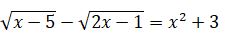تەڭدەۋىن شەشىڭىز.

شەشۋى.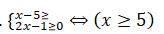

تەڭسىزدىكتەر جۇيەسى دەپ قاراستىرساق، قاتە جىبەرگەن بولار ەدىك. سەبەبى تەڭدەۋدىڭ وڭ جاق بولىگى ەسكەرىلمەي وتىر. ول نولدەن ۇلكەن، سوندىقتان تەڭدەۋدىڭ انىقتالۋ وبلىسى كەلەسى تەڭسىزدىكتەر جۇيەسىنىڭ شەشىمى بولادى:

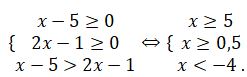
دەمەك، تەڭدەۋدىڭ شەشىمى جوق.

5. 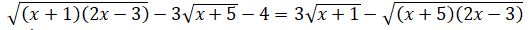 تەڭدەۋىن شەشەمىز.

شەشۋى. تەڭدەۋدىڭ ەكى جاعىن كۆادراتتاساق بەرىلگەن تەڭدەۋدەن دە كۇردەلى تەڭدەۋ الامىز. سوندىقتان، بەرىلگەن تەڭدەۋدى كەلەسىدەي تۇرلەندىرەيىك: 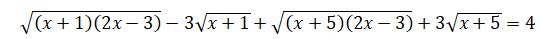تەڭدەۋدىڭ coل جاعىنداعى ورنەكتى كوبەيتكىشتەرگە جىكتەسەك  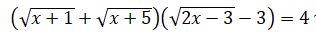تەڭدەۋىنە كەلەمىز. ادەتتە، تەندەۋدىڭ وڭ جاعىندا 0 بولعاندا كوبەيتكىشتەرگە جىكتەيدى. بەرىلگەن تەڭدەۋ جاعدايىندا كوەففيسەنتتەرگە بايلانىستى، تەڭدەۋدىڭ شەشىمى جەڭىل تابىلادى. سوڭعى تەڭدەۋدىڭ ەكى جاعىن دا ءبىرىنشى جاقشاداعى ورنەكتىڭ تۇيىندەسىنە كوبەيتەيىك، ياعني،  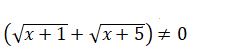ورنەگىنە. وندا  

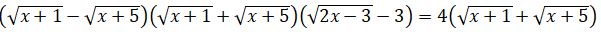وسىدان  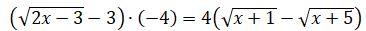نەمەسە  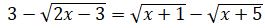بولادى. سوڭعى تەڭدەۋدىڭ ەكى جاعىن دا كۆادراتتاساق  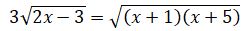تەڭدەۋىنە كەلەمىز. باسقاشا توپتاستىرىپ كۆادراتتاۋ، بەرىلگەن تەڭدەۋدەن دە كۇردەلى تەڭدەۋگە اكەلەدى. سوڭعى تەڭدەۋدىڭ ەكى جاعىن دا كۆادراتتاپ،

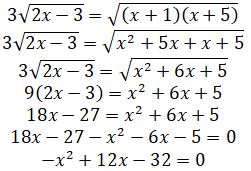
x² -12x +32 = 0 تەڭدەۋىن الامىز. وسىدان، x = 8 جانە x = 4. تابىلعان شەشىمدەردى تەڭدەۋگە قويىپ تەكسەرىپ، ونىڭ شەشىمى x = 8 ەكەندىگىن كورەمىز.

يرراسيونال تەڭدەۋلەر مەن تەڭسىزدىكتەردى شەشۋدىڭ جولدارىن تالداۋدا مەكتەپ ماتەماتيكاسىنىڭ نەگىزگى تەوريالىق ماتەريالى قامتىلادى. تاقىرىپتى دۇرىس مەڭگەرۋ ءۇشىن تەڭدەۋلەر كلاسسيفيكاسيالانىپ، ولاردىڭ ءارقايسىسى بويىنشا ونى شەشۋدىڭ ادىس-تاسىلدەرى تاڭدالىپ، مەڭگەرىلۋ دەڭگەيى تەكسەرىلەتىندىگى بەلگىلى. مۇقيات ىرىكتەلىپ، مۇمكىندىگىنشە تولىق باياندالعان تەوريالىق ماتەريال، ەسەپ قويىلىمىن جانە ونى شەشۋدىڭ تاسىلدەرىن ۇيرەنۋدى قامتاماسىز ەتۋمەن قاتار، قاتاڭ لوگيكالىق تالداۋلاردى مەڭگەرۋدە دە سەپتىگى تيەر دەگەن ويدامىز.

پايدالانعان ادەبيەتتەر:

1. «سامۇرىق» ماتەماتيكالىق زياتكەرلىك سايىسىنا بەرىلگەن ەسەپتەردى شىعارۋعا ارنالعان ادىستەمەلىك قۇرال (5-7 سىنىپ)
2. ا. ي پريلەپكو «سبورنيك زاداچ پو ماتيماتيكە» موسكۆا، 1983
3. ز. ك اينازاروۆا «سپراۆوچنيك شكولنيكا پو ماتەماتيكە»، «ارمان-پۆ»، 2007ج

---